Les dômes géodésiques

Voici une image d’un dôme géodésique fréquence 2.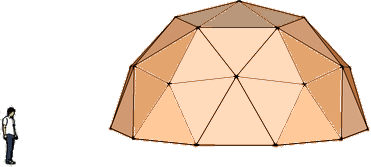 

Dome géodésique

L’invention du dôme geodésique est crédité de Buckminster Fuller , mais aurait été inventé 25 ans plus tôt par Walter Bauerfeld pour le travail sur un projecteur planétarium à optique Carl Zeiss.

 

La géométrie du dôme géodésique

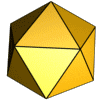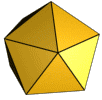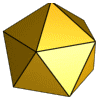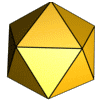
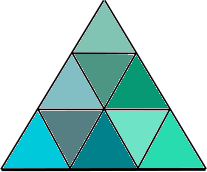
Les dômes géodésiques  le plus populaire est basée sur un icosaèdre dont les faces triangulaires sont ensuite subdivisés en petits triangles. Un icosaèdre a vingt faces, dont chacune est un triangle équilatéral et donc tous les triangles sont de la même taille. Comme vous pouvez le voir sur la photo ci-dessous, un icosaèdre a une base composée de cinq triangles tout en partageant les points haut et bas, respectivement. Dix triangles relient le couvercle et la base. Wikipedia a une page assez vaste et déconcertant à propos de icosaèdres .

Isocaèdre

La géometrie composé de triangles est structurellement très forte. Si vous vous penchez sur l’un des coins d’un triangle formé de trois tubes boulonnés entre eux, la seule façon de s’effondrer, c’est que l’un des tube casse C’est beaucoup plus fort qu’un rectangle, un rectangle de tubes  pourrait s’effondrer par le glissement sur les boulons.

La force placé dans un coin d’un triangle est directement transmise à la base du triangle. Depuis un icosaèdre est composé de triangles, la force est répartie tout au long de la forme.L’icosaèdre est une structure très solide.

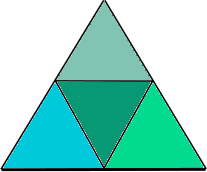
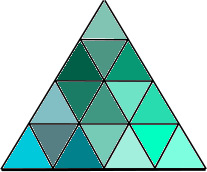
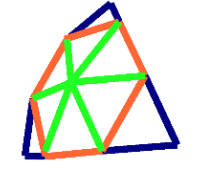
Les triangles qui constituent l’icosaèdre sont subdivisés en fractionnant les cotés du triangle, puis procéder à de nouvelles division en plus de triangles. Comme dans les images ci-dessous, le fractionnement de chaque coté en n nouveaux cotés crée n ² nouveaux triangles.

Un triangle dont les côtés sont divisés en 2, le résultat est de 4 triangles

Un triangle dont les côtés sont divisés en 3, le résultat est de 9 triangles

Un triangle dont les côtés sont divisés en 4, le résultat est de 16 triangles

On note mV , où m est le nombre de nouveaux cotés fabriqués à partir de chaque coté original, comme 2v , 3v , 4v , etc ..

Si les angles des nouveaux triangles sont ensuite déplacés vers la surface d’une sphère centrée sur l’icosaèdre, vous obtenez quelque chose qui ressemble de plus en plus à une sphère, le plus si les triangles sont beaucoup divisés. Ceux-ci sont appelés «sphères géodésiques ». Voici les sphères géodésiques où les arêtes initiales sont divisées en deux ( soit 80 triangles), trois (180 nouveaux triangles), et quatre (320 nouveaux triangles).En divisant chaque segment initial en 10 nouveaux bords, on obtient 2000 triangles, 100 pour chaque triangle original sur l’icosaèdre.

sphère géodésique 2v (80 triangles)		sphère géodésique 3v (180 triangles)

sphère géodésique 4v (320 triangles)		sphère géodésique 10v (2000 triangles)

Pour faire un dôme géodésique, vous coupez une sphère géodésique de moitié.

Les sphères avec un degré impair (1v, 3v, 5v, etc ..) ne peuvent pas réellement être coupés exactement à la moitié. Il y a un anneau de triangles qui couvrent le centre de la sphère, donc généralement vous choisissez de scinder soit juste au-dessus ou en dessous de cette bague. Pour les dômes 3v, l’appellation sera «3/8» et «5/8″, respectivement. Voici les photos de dômes géodésiques 3/8 3V, 5/8 3V, les 4V, et les 5v.

La construction d’un dome

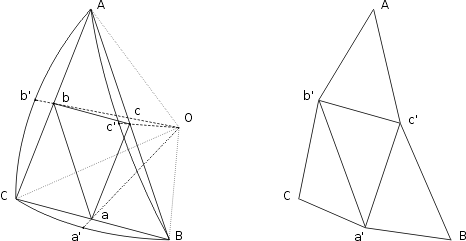
Une chose intéressante à propos du processus de division des triangles, c’est que les arretes ne sont plus de longueurs égales. Ainsi, les triangles ne sont plus équilatéraux. Le calcul est un peu compliqué à obtenir. (Il y a des programmes pour le faire.) Image ci-dessous d’un seul triangle 3v avant et après projection sur la sphère incluant les nouvelles longueurs si le triangle d’origine était de 3 mètres de chaque côté.

Longueurs d’arêtes des triangles projetés

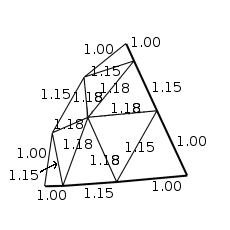
C’est pourquoi des sites comme Dômes du désert sont si utiles aux constructeurs de dôme, le site des Dômes du désert fournit les rapports de longueurs de jambe de force pour les dômes les plus courants.

Vous pouvez voir qu’il n’y a que trois longueurs uniques, 1.00, 1.15, et 1.18 mètres. Une façon de fournir un modèle facile pour la construction d’un dôme avec un code de couleur des arrêtes,  fournir un schéma de de visualisation du dôme final avec classement des arrêtes par couleur. Par exemple, une couleur pour les  entretoises 1,18 mètres vert, le 1,15 mètre entretoises orange, et les montants de 1 mètre bleu.

si vous voulez un dôme « 5/8 »  fréquence 3 avec entretoises de 1, 1,15 et 1,18 mètres, le dôme serait de 5,7 mètres de diamètre.

Voici une paire d’images montrant un de dômes 5/8 fréquence 3 avec entretoises de couleur assortie.

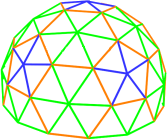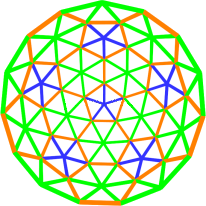Vue de profil		Vue de dessus

Cette structure est en connexion avec la terre et elle est donc utilisée pour des fonctions d’ancrage, de reconnexion avec ses racines.

Elle est donc particulièrement bénéfique pour l’habitat familial avec enfant.

Elle facile à chauffer l’hiver avec un poêle et ne consomme pas beaucoup de bois.